Question

A 7.27- kilogram bowling ball is rotating at a 15.2 revolutions per second. A bowling ball has a diameter of 21.6 centimeters. Tom touches the spinning ball with his finger to stop the ball from rotating. How much force must be applied to the surface of the bowling ball to stop its rotation in 0.525 seconds?

Answer 1

angular speed of the ball = 15.2 rev/s

diameter = 21.6 cm

radius = 10.8 cm

mass = 7.27 kg

Moment of inertia of ball is given as

`I = (2)/(5)mR^2`

`I = (2)/(5)\time 7.27* (0.108)^2`

`I = 0.034 kg m^2`

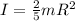
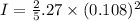
now angular acceleration is defined as rate of change in angular velocity

`\alpha = (\omega_f - \omega_i)/(t)`

`\alpha = (2\pi (15.2) - 0)/(0.525)`

`\alpha = 182 rad/s`

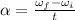
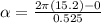
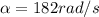
now we know that

`\tau = I \alpha`

`\tau = 0.034 * 182 = 6.18 Nm`

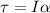
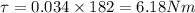
so it requires a torque of 6.18 Nm