Question

If x + 4y = 18 and x − 4y = 2, then x = ?

Answer 1

x + 4y = 18 and x − 4y = 2

I would use substitution

add the 2 equations together

x + 4y = 18

+ x − 4y = 2

-------------------------

2x + 0y = 20

2x = 20

divide each side by 2

2x/2 = 20/2

x = 10

Answer: x=1

Answer 2

x=10

Explanation:

We have the system
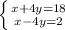`\left \{ {{x+4y=18} \atop {x-4y=2}} \right.` and we have to find the value of x,

we can clear y from both equations and then match them.

First equation:

`x+4y=18\\4y=18-x\\y=(18-x)/(4)`

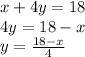
Second equation:

`x-4y=2\\4y=x-2\\y=(x-2)/(4)`

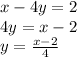
Now matching both equations:

`y=y\\(18-x)/(4)=(x-2)/(4)\\18-x=x-2`

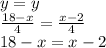
We can subtract x in both sides,

`18-x=x-2\\18-x-x=x-2-x\\18-2x=-2`

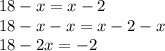
Subtract 18 in both sides,

`18-2x=-2\\18-2x-18=-2-18\\-2x=-20`

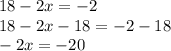
Divide both sides in (-2),

`-2x=-20\\(-2x)/(-2) =(-20)/(-2)\\ x=10`

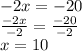
Result: x=10