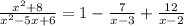Question

X^2+8/x^2-5x+6 expressed as partial fractions

Answer 1

yee, partial fractions

remember some things to solve:

`(px+q)/((x+a)(x+b))=(A)/(x+a)+(B)/(x+b)`

`(px+q)/((x+a)^2)=(A)/(x+a)+(B)/((x+a)^2)`

`(px^2-qx+r)/((x+a)(x^2+bx+c))=(A)/(x+a)+(Bx+C)/(x^2+bx+c)`

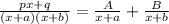
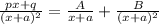
for your problem

`(x^2+8)/(x^2-5x+6)`

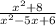
by long division, we get
`1+(5x+2)/(x^2-5x+6)`

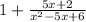
let's consider the 2nd part

`(5x+2)/(x^2-5x+6)`

factor

`(5x+2)/((x-3)(x-2))`

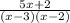
apply thing

`(5x+2)/((x-3)(x-2))=(A)/(x-3)+(B)/(x-2)`

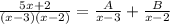
solve for A and B

cross multiply

5x+2=A(x-2)+B(x-3)

5x+2=Ax-2A+Bx-3B

match powers

5x=Ax+Bx

5=A+B

2=-2A-3B

adding twice of previous equation, we get

12=-B

B=12

5=A+B

5=A+12

-7=A

so expressed as partial fractions, it is
`(x^2+8)/(x^2-5x+6)=1-(7)/(x-3)+(12)/(x-2)`