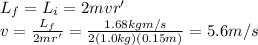Question

1) Hickory dickory dock, the 20.0-g mouse ran up the clock, and took turns riding on the 0.20-m-long second hand, the 0.20-m-long minute hand and the 0.10-m-long hour hand. What was the angular momentum of the mouse on each of the three hands?

2) In a physics experiment, Ingrid, the ice skater, spins around in the rink at 1.2 m/s with each of her arms stretched out 0.70m from the center of her body. In each hand she holds a 1.0kg mass. If angular momentum is conserved, how fast will Ingrid beging to spin if she pulls her amrs to a position 0.15m from the center of her body?

Answer 1

1a) Angular momentum of the mouse on the second hand:
`8.4\cdot 10^(-5) kg m^2/s`

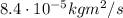
The angular momentum of the mouse is given by:

`L=mvr`

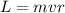
where

m = 20.0 g = 0.02 kg is the mass of the mouse

v is the speed of the mouse

r = 0.20 m is the length of the hand

The speed of the mouse is equal to the length of the circumference divided by the time taken to complete one circle (60 s):

`v=(2\pi r)/(t)=(2\pi (0.20 m))/(60 s)=0.021 m/s`

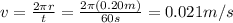
So the angular momentum is

`L=mvr=(0.02 kg)(0.021 m/s)(0.2 m)=8.4\cdot 10^(-5) kg m^2/s`

1b) Angular momentum of the mouse on the minute hand:
`1.4\cdot 10^(-6) kg m^2/s`

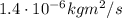
In this case, the mouse takes
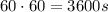`60\cdot 60=3600 s` to complete one circle, so the speed of the mouse is

`v=(2\pi r)/(t)=(2 \pi (0.20 m))/(3600 s)=3.5\cdot 10^(-4) m/s`

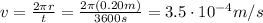
So, the angular momentum is

`L=mvr=(0.02 kg)(3.5\cdot 10^(-4) m/s)(0.20 m)=1.4\cdot 10^(-6) kg m^2/s`

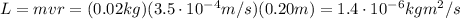
1c) Angular momentum of the mouse on the hour hand:
`3\cdot 10^(-8) kg m^2/s`

In this case, the mouse takes
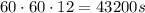`60\cdot 60 \cdot 12=43200 s` to complete one circle, so the speed of the mouse is

`v=(2\pi r)/(t)=(2 \pi (0.10 m))/(43200 s)=1.5\cdot 10^(-5) m/s`

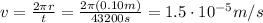
So, the angular momentum is

`L=mvr=(0.02 kg)(1.5\cdot 10^(-5) m/s)(0.10 m)=3\cdot 10^(-8) kg m^2/s`

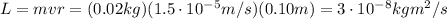
2) New speed of Ingrid: 5.6 m/s

The initial angular momentum of Ingrid is twice the momentum produced by each mass:

`L_i=2 mvr = 2(1.0 kg)(1.2 m/s)(0.70 m)=1.68 kg m/s`

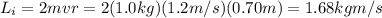
Angular momentum must be conserved, so the final momentum must be the same when the arms are pulled to a new length of r'=0.15 m, so we find:

`L_f = L_i = 2 mv r'\\v=(L_f)/(2mr')=(1.68 kg m/s)/(2(1.0 kg)(0.15 m))=5.6 m/s`