Answers:
Two triangles are congruent if they have the same sides and the same size.
In other words: they have the same shape and size, regardless of their position or orientation.
If we want to verify if two triangles are congruent, they must fulfill some conditions:
a) Two triangles are congruent if their three sides are respectively equal
b) Two triangles are congruent if two of their sides and the angle between them are respectively of equal length.
c) Two triangles are congruent if they have a congruent side and the angles with vertex at the ends of that side are also congruent.
d) Two triangles are congruent if they have two sides respectively congruent and the angles opposite the greater of the sides are also congruent
According to these criteria, it is not necessary to verify the congruence of the three sides and three angles of each triangle
Now, knowing these criteria, let’s answer the questions:
1) Here both triangles are congruent and are Right Triangles (have a right angle or a
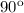 angle), as well.
angle), as well.
This means angle
 and according to the criterion b listed above, the angle
and according to the criterion b listed above, the angle
 and angle
and angle
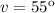 .
.
This can be proven by the rule that states the sum of the three interior angles of a triangle is
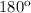 .
.
Then, according criterion a,
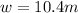 and
and
 .
.
This can be proven by the use of two trigonometric functions, sine and cosine:
 (1)
(1)
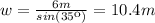
Where
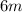 is the Opposite side to the
is the Opposite side to the
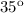 angle and
angle and
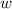 is the hypotenuse.
is the hypotenuse.
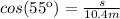 (2)
(2)
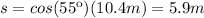 ≅6m
≅6m
Where
 is the Adjacent side to the
is the Adjacent side to the
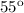 angle and
angle and
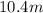 is the hypotenuse.
is the hypotenuse.
Therefore, the answer is B:
 ,
,
 ,
,
 ,
,
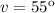 ,
,
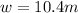
2) According to the second figure shown, both triangles are congruent and fulfill the four criteria described above.
Therefore, the answer is:
CBA≅MPN
3) “Knowing that line segment AB is the same length as line segment CD is enough to prove that triangles ABD and BCD are congruent”
This statement is True, because both triangles share the line segment BD.
This means they have two equal sides, and according to criterion b they are congruent