Question

Ten people can dig five holes in three hours. If n people digging at the same rate dig m holes in d hours:

1.Is n proportional to m when d=3?
2.Is n proportional to d when m=5?
3.Is m proportional to d when n=10?

Answer 1

3 beacuse just beacause

Explanation:

Answer 2

First. get the unit rate. That is, transform "Ten people can dig five holes in three hours" into "One person digs one holes in one hour."

We can say that

`\frac{5\,\mbox{holes}}{3\,\,\mbox{hours}\cdot\mbox{10\,\,\mbox{person}}}=\frac{(5)/(3)\,\,\mbox{holes}}{1\,\,\mbox{hour}\cdot\mbox{10\,\,\mbox{person}}}`

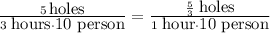
(that's still for 10 people). For 1 person this rate will be 1/10th of the above, so:

`\frac{(5)/(3)\,\,\mbox{holes}}{1\,\,\mbox{hour}\cdot 10 \,\,\mbox{person}}=\frac{(5)/(30)\,\,\mbox{holes}}{1\,\,\mbox{hour}\cdot 1 \,\,\mbox{person}}`

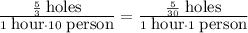
So the unit rate is 5/30. We can now set up an equation expressing the number of holes "m" dug up by "n" people in "d" hours:

`m = (5)/(30)\cdot n\cdot d`

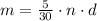
which is clearly linear in n and d.

Now we can answer the questions:

(1) Is n proportional to m when d=3? Answer: Yes

`m = (5)/(30)\cdot n \cdot 3 = (1)/(2)n\\\implies n = 2m`

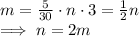
which shows that n is proportional to m in this case.

(2) Is n proportional to d when m=5? Answer: No

`5 = (5)/(30)\cdot n \cdot d\\\implies n = (30)/(d)`

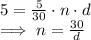
There is an inverse proportionality, therefore this is not proportional.

(3) Is m proportional to d when n=10? Answer: Yes

`m = (5)/(30)\cdot 10 \cdot d = (5)/(3)d`

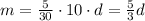
There is a proportional relationship between m and d.