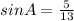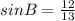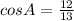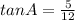Question

Right triangle ABC has its right angle at C.

AC=12 and BC=5 .

Which trigonometric ratios are correct?

Select each correct answer.




cosA=12/13

tanA=12/13

tanB=5/12

sinB=12/13

sinA=5/13

Answer 1

CosA=12/13

SinB=12/13

SinA=5/13

Explanation:

I took the test :)

Answer 2

The answers are:

`cosA=(12)/(13)`

`sinB=(12)/(13)`

`sinA=(5)/(13)`

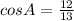
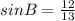
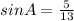
The explanation is shown below:

1. By definition, when you have a rigth triangle, you can find the sine, cosine and tangent as following:

`sine=(opposite)/(hypotenuse)\\cosine=(adjacent)/(hypotenuse)\\tangent=(opposite)/(adjacent)`

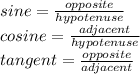
3. To know the lenght of the hypotenuse you can apply the Pythagorean Theorem:

`hypotenuse=\sqrt{12^(2)+5^(2)}=13`

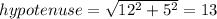
4. Therefore if AC=12, BC=5 and the right angle is at C, you can substitute values to find the sine, cosine and tangent of A and B:

`sinA=(5)/(13)`

`sinB=(12)/(13)`

`cosA=(12)/(13)`

`cosB=(5)/(13)`

`tanA=(5)/(12)`

`tanB=(12)/(5)`