Question

Check my answer(there’s one above) I really just chose my best guess on this.for the ones below, can you provide a simple explanation and the answer? Please help me...

What is the length of a stopped pipe that has a fundamental frequency of 153 Hz when the speed of sound is 340 m/s?
28 cm
43 cm
56 cm
2.1 cm
17 cm
For an open pipe of length L, what are the possible wavelengths of a standing wave? (Let n = a time positive integer)
2L/3n
Ln
L/n
2L/n
A standing wave of the third harmonic is induced in a stopped pipe. The speed of sound through the air of the pipe is 340 m/s, and the frequency of the wave is 235 Hz. What is the length of the pipe?
133 cm
189 cm
109 cm
124 cm
WARNING IF YOU ANSWER JUST FOR FREE POINTS, I WILL REPORT YOU AND THEY WILL BE TAKEN AWAY.

Answer 1

#1

For closed pipe the fundamental frequency will be given as

`f = (v)/(4L)`

`153 = (340)/(4L)`

`L = 0.56 m`

`L = 55 cm`

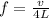
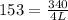
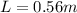
#2

For open pipe the wavelength for Nth harmonic will be given as

`n * (\lambda)/(2) = L`

`\lambda = (2L)/(n)`

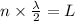
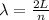
#3

for a closed pipe the frequency is given as

`f = (nv)/(4L)`

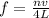
here for third harmonic n = 3

`f = (3v)/(4L)`

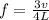
now plug in all values

`235 = (3* 340)/(4L)`

`L = 1.09 m`

`L = 109 cm`

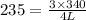
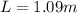
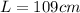
#10

since in the given figure there are three complete loops

so in this case the number of harmonics are THREE