Question

Quadratic equations and complex numbers PLEASE HELPPPP ASAP

Answer 1

we are given

`27x^3-1=0`

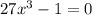
we can also write it as

`(3x)^3-(1)^3=0`

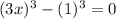
now, we can use factor formula

`a^3-b^3=(a-b)(a^2+ab+b^2)`

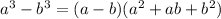
we can use above formula

we get

`(3x)^3-(1)^3=(3x-1)((3x)^2+3x* 1+(1)^2)`

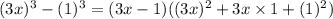
now, we can simplify it

`27x^3-1=(3x-1)(9x^2+3x+1)`

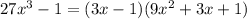
now, we can set it to 0

`27x^3-1=(3x-1)(9x^2+3x+1)=0`

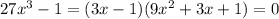
and then we can solve for x

`(3x-1)(9x^2+3x+1)=0`

`3x-1=0`

`x=(1)/(3)`

`9x^2+3x+1=0`

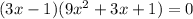
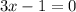
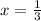
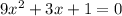
now, we can use quadratic formula

`x=(-b\pm √(b^2-4ac))/(2a)`

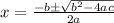
now, we can plug values

and we get

`x=(-3\pm √(3^2-4\cdot \:9\cdot \:1))/(2\cdot \:9)`

`x=-(1)/(6)+i(√(3))/(6),\:x=-(1)/(6)-i(√(3))/(6)`

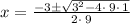
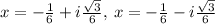
So, we will get solution as

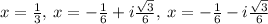`x=(1)/(3),\:x=-(1)/(6)+i(√(3))/(6),\:x=-(1)/(6)-i(√(3))/(6)`...............Answer