Question

Please help with Qudratic equations and complex numbers

Answer 1

19. 7, 14 and 24

20. 2 seconds

Explanation:

Question 19:

We have a triangle with perimeter 45cm.

Assuming its shortest side to be x, we can write expressions for each of its sides and form an equation.

shortest side ---> x

one side is twice as long as the shortest side ---> 2x

remaining side is 25cm less than the square of the shortest side ---> x^2-25

Combing these to get:

`x+2x+(x^2-25)=45\\\\x^2+2x+x-25-45=0\\\\x^2+3x-70=0`

Now factorizing this quadratic equation to get:

`x^2-7x+10x-70=0\\\\x(x-7)+10(x-7)=0\\\\(x-7)=0, (x+10)=0\\\\x=7,x=-10(ignore)`

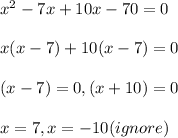
Therefore, the lengths of three sides of this triangle are:

x ---> 7

2x ---> 2*7 ---> 14

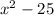`x^2-25` ---> (7*7)-25 ---> 24

Question 20:

The height h (in feet) of the rock after t seconds is given by the equation:

`h=-16t^2+144`

a) initial height of the rock = 144 feet

b) Putting h = 80 to find the the seconds after the rock is dropped will it be 80 feet above the water.

`80=-16t^2+144`

`16t^2=144-80`

`16t^2=64`

`t^2=4`

`t=2`

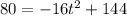
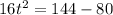
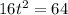
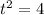
The time will be 2 seconds.

Answer 2

Let sides of triangle be a,b,c in cm.

Then perimeter=a+b+c = 45 ... i

a= 2b... ii

`c = b^2-25`... iii

Let us substitute a=2bin i.We get 3b+c = 45

Or c = 45-3b :

(45-3b) =
`c = b^2-25`

`b^2+3b-70=0(b+10)(b-7)=0\\b cannot be negative\\b= 7`

a= 14 and c = 24

But since a+b <c, this cannot form a triangle.

Hence no solution.

--------------------------------

h(0) = initial height = 144 ft.

b) When h = 80,

we have
`80 = -16t^2+144\\16t^2 = 64\\t =2`

After 2 seconds.