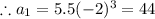Question

A geometric sequence is shown below:

Answer 1

A) Common Ratio (r) = -2

B)
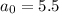`a_0=5.5` and
`a_1=-44`

Explanation:

We are given a geometric series with some missing term.

Common ratio of geometric series is ratio two consecutive term.

Common ratio (r) =
`(22)/(-11)=-2`

Now we find the missing term.

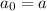`a_0=a` First term of the series.

Common ratio r=-2

So,
`(-11)/(a)=-2`

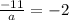
So, a=5.5

`\therefore a_0=5.5`

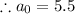
Now we find second missing term
`a_(1)`. This 4th term of the series

So,
`a_1=ar^3`

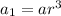
where, a=5.5 and r=-2

`\therefore a_1=5.5(-2)^3 = 44`