Question

L (-1,-1)

M (0,0)
N (3,0)
Parallelogram LMNO has the coordinates shown.
Find the coordinates of point O.
A) (1,-1)
B) (2,-1)
C) (2,0)
D) (2,1)

Answer 1

The answer is B) (2,-1).If you don’t believe me punch in the coordinates into a graphing calculator and then punch in (2,-1). It will give you a perfect parallelogram.

Answer 2

Answer: The correct option is (B) (2, -1).

Step-by-step explanation: Given that LMNO is a parallelogram where the co-ordinates of the vertices L,M and N are

L(-1,-1) , M(0,0) and N(3,0).

We are to find the co-ordinates of the vertex O.

Let, (a, b) be the co-ordinates of the vertex O.

Since LMNO is parallelogram, so the opposite sides will be parallel.

That is, LM is parallel to NO. So, we have

`\textup{slope of LM}=\textup{slope of NO}\\\\\Rightarrow (0-(-1))/(0-(-1))=(b-0)/(a-3)\\\\\\\Rightarrow (1)/(1)=(b)/(a-3)\\\\\Rightarrow b=a-3\\\\\Rightarrow a=b+3~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

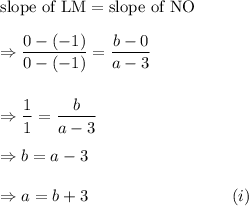
and MN is parallel to OL. So,

`\textup{slope of MN}=\textup{slope of OL}\\\\\\\Rightarrow (0-0)/(3-0)=(-1-b)/(-1-a)\\\\\\\Rightarrow 0=(b+1)/(a+1)\\\\\\\Rightarrow b+1=0\\\\\Rightarrow b=-1.`

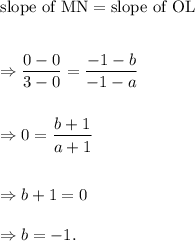
Therefore, from equation (i), we get

`a=-1+3=2.`

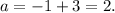
Thus, the co-ordinates of vertex O are (2, -1).

Option (B) is correct.