Question

Identify the type of sequence shown in the table below and select the appropriate response. n f(n) 1 48 2 −96 3 192 4 −384 5 768 Arithmetic sequence; common difference is 96 Arithmetic sequence; common difference is −144 Geometric sequence; common ratio is 3 Geometric sequence; common ratio is −2

Answer 1

This is a geometric sequence with common ratio r = - 2

r =
`(-96)/(48)` =
`(192)/(-96)` =
`(-384)/(192)` = - 2

Answer 2

the sequence is geometric sequence with common ratio (-2).

Option : D is correct.

Explanation:

In this question table is given as

n 1 2 3 4 5

f(n) 48 -96 192 -385 768

We have to find out if the sequence is arithmetic or geometric.

For Arithmetic sequence :

Difference should be common in each term of fees.

common difference
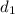`d_(1)` = f(2) - f(1)

= -96 -48 = -144

similarly
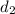`d_(2)` = f(3) - f (2) = 192 + 96 = 288

Here,
`d_(1)` ≠
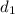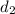`d_(2)` so the sequence is not an arithmetic sequence.

For Geometric sequence :

Ratio should be common in each term of f(n)

Common ratio
`r_(1)` =
`(f(2))/(f(1))=(-96)/(48)=(-2)`

`r_(2)=(f(3))/(f(1))=(192)/((-96))=(-2)`

`r_(1)=r_(2)`

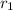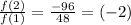
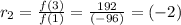
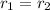
Therefore, the sequence is geometric sequence with common ratio (-2).

Option : D is correct.