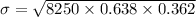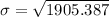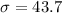Question

A binomial distribution of 8,250 trials has a probability of p=0.638. What is the standard deviation?

A: 43.7
B: 0.2
C: 5,263.5
D: 1,905.4

Answer 1

43.7

Explanation:

Answer 2

ANSWER

The standard deviation is

`43.7`


EXPLANATION


The standard deviation of a binomial distribution can be calculated using the formula,


`\sigma = √(n * p * q)`


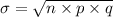
where,

`n`
is the number of trials,

`p`

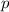
is the numerical probability of a success and

`q`
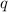
is the numerical probability of a failure.


From the question

`n = 8250`



`p = 0.638`

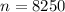
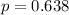
and

`q = 1 - 0.638 = 0.362`

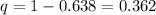
We substitute all these values into the formula and simplify to obtain,


`\sigma = √(8250* 0.638 * 0.362)`




`\sigma = √(1905.387)`




`\sigma = 43.7`