Question

Malory isn’t putting money in two savings accounts.Account A started with $150 and Account B started with $300.Malory deposits $16 in Account A and $12 in Account B each month.In how many months will Account A have a balance at least as great as Account B?What will that balance be?

Answer 1

Given:

• There are two savings accounts - account A has $150 and account B has $300 to begin with.
• Malorie deposits $16 in account A and $12 in account B every month.

To Find:

The number of months where the balance of both is equal and the balance itself.

Solution:

In 37.5 months, the account balances in both accounts will be equal.

This balance will be equal to $750 in both account A and B.

Calculation:

Let x be the number of months where both the accounts have equal balance.

So, at the end of x months, 16x is the amount of money that will be added to account A (since $16 is added every month).

And the total amount at the end of x months will therefore be $(150+16x)

Similarly, at the end of x months, 12x is the amount of money that will be added to account B (since $12 will be added every month).

And the total amount at the end of x months will therefore be $(300+12x)

By our assumption, x is the number of months it will take for both the accont balances will be equal. Therefore, we have the equation

`150+16x=300+12x\\4x=150\\x=37.5`

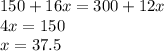
Therefore, in 37.5 months, the account balances in both accounts will be equal.

This balance will be equal to
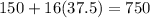`150+16(37.5)=750` i.e. $750 will be the balance in both account A and B.