If events X and Y are independent, what must be true? Check all that apply. P(Y | X) = 0 P(X | Y) = 0 P(Y | X) = P(Y) P(Y | X) = P(X) P(X | Y) = P(Y) P(X | Y) = P(X)

Question

asked Jun 28, 2019 92.1k views

2 Answers

Pat Morin · Answer 1 · 2019-07-02T15:05:57+0000

if events X and Y are independent, then for intersection we multiply the probability

P(Y∩X) = P(Y) * P(X)

We know that

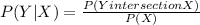
P(Y|X) =(P(YintersectionX))/(P(X))

Now we replace P(Y) * P(X) for P(Y∩X)

P(Y|X) =(P(Y)*P(X))/(P(X))

Cancel out P(X)

So

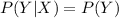
Like that

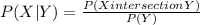
P(X|Y) =(P(XintersectionY))/(P(Y))

Now we replace P(X) * P(Y) for P(X∩Y)

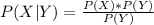
P(X|Y) =(P(X)*P(Y))/(P(Y))

Cancel out P(Y)

So

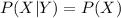
P(Y | X) = P(Y) and P(X | Y) = P(X) are true