Question

What is the explicit rule for the sequence 3, –6, 9, –18, 36, ...?

A. an =2(–3)n–1
B. an =3(2)n–1
C. an =3(–2)n
D. an =3(–2)n–1

Answer 1

I’m not quite sure, but I believe the answer to be either A or C.

Answer 2

D.
`a_n =3(-2)^(n-1)`

Explanation:

Let's try each rule with some numbers:

Rule A.
`a_n=2(-3)^(n-1)`

`n=1, a_n=2(-3)^(1-1)=2(-3)^(0)=2(1)=2`

`n=2, a_n=2(-3)^(2-1)=2(-3)^(1)=2(-3)=-6`

`n=3, a_n=2(-3)^(3-1)=2(-3)^(2)=2(9)=18`

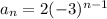
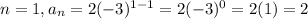
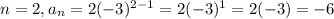
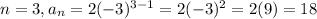
Rule B.
`a_n =3(2)^(n-1)`

`n=1, a_n=3(2)^(1-1)=3(2)^(0)=3(1)=3`

`n=2,a_n=3(2)^(2-1)=3(2)^(1)=3(2)=6`

`n=3, a_n=3(2)^(3-1)=3(2)^(2)=3(4)=12`

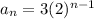
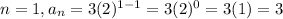
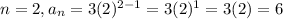
Rule C.
`a_n =3(-2)^n`

`n=1, a_n=3(-2)^1=3(-2)=-6`

`n=2,a_n=3(-2)^2=3(4)=12`

`n=3,a_n=3(-2)^3=3(-8)=-24`

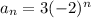
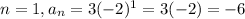
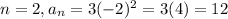
Rule D.
`a_n =3(-2)^(n-1)`

`n=1, a_n =3(-2)^(1-1)=3(-2)^(0)=3`

`n=2,a_n =3(-2)^(2-1)=3(-2)^(1)=3(-2)=-6`

`n=3,a_n =3(-2)^(3-1)=3(-2)^(2)=3(4)=12`

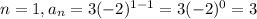
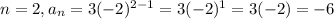
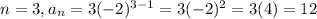
The only rule that has two consecutive values of the sequence when evaluated and starts with 3 is the rule D, first has a 3 and then a -6. It is the rule that generates the most similar sequence.