Since M is the midpoint of segment CP, BM is the median of the triangle PBC.
Note that median of a triangle divides it into two triangles of equal area.
Therefore, area (BCP) = 2 × area (BMP)
Given that area (BMP) = 21
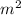
So, area (BCP) = 2 × 21 = 42
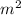 --- (1)
--- (1)
Let h be the height of triangle ABC from the vertex C.
Then, area of Δ ABC =

Area of Δ BCP =
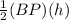
Also, since AP : BP = 1 : 3,
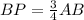
So, area of Δ BCP =
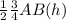
But, from (1) area (BCP) = 42
Therefore,
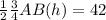
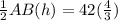
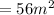
Hence, area of Δ ABC =
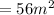 .
.