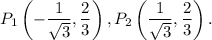Question

find the coordinates of the point P on the parabola y=1-x^2 with domain 0≤x≤1 that minimize the area of the triangle enclosed by the tangent line at P, the x-axis, and y-axis

Answer 1

Let point P be with coordinates
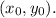`(x_0,y_0).` Find the equation of the tangent line.

1. If
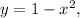`y=1-x^2,` then
`y'=-2x.`

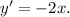
2. The equation of the tangent line at point P is

`y-y_0=-2x_0(x-x_0).`

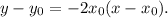
Find x-intercept and y-intercept of this line:

• when x=0, then
  `y=y_0+2x_0^2;`
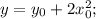
• when y=0, then
  `x=(y_0)/(2x_0)+x_0=(y_0+2x_0^2)/(2x_0).`

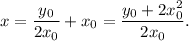
The area of the triangle enclosed by the tangent line at P, the x-axis, and y-axis is

`A=(1)/(2)\cdot (2x_0^2+y_0)\cdot \left((y_0+2x_0^2)/(2x_0)\right)=((y_0+2x_0^2)^2)/(4x_0).`

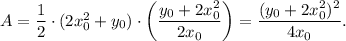
Since point P is on the parabola, then
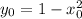`y_0=1-x_0^2` and

`A=((1-x_0^2+2x_0^2)^2)/(4x_0)=((1+x_0^2)^2)/(4x_0).`

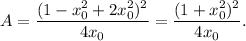
Find the derivative A':

`A'=(2(1+x_0^2)\cdot 2x_0\cdot 4x_0-4(1+x_0^2)^2)/(16x_0^2)=(12x_0^4+8x_0^2-4)/(16x_0^2).`

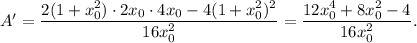
Equate this derivative to 0, then

`12x_0^4+8x_0^2-4=0,\\ \\3x_0^4+2x_0^2-1=0,\\ \\D=2^2-4\cdot 3\cdot (-1)=16,\ √(D)=4,\\ \\x_0^2_(1,2)=(-2\pm4)/(6)=-1,(1)/(3),\\ \\x_0^2=(1)/(3)\Rightarrow x_0_(1,2)=\pm(1)/(√(3)).`

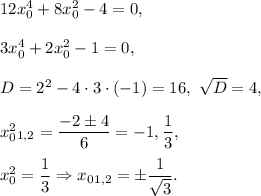
And

`y_0=1-\left(\pm(1)/(√(3))\right)^2=(2)/(3).`

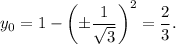
Answer: two points:
`P_1\left(-(1)/(√(3)),(2)/(3)\right), P_2\left((1)/(√(3)),(2)/(3)\right).`