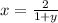Question

7x + 3y = m

Solve for y

4(r + 3) = t

Solve for r

2x + b = w

Solve for x

x(1 + y) = 2

Solve for x

Answer 1

7x + 3y = m

3y = m - 7x

y = (m - 7x) / 3

4( r + 3 ) = t

r + 3 = t / 4

r = ( t - 3 )/ 4

2x + b = w

2x = w- b

x = ( w - b ) / 2

x (1 + y) = 2

x = 2 / 1 +y

Answer 2

QUESTION 1

The given equation is


`7x + 3y = m`

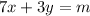
We want to solve for y in the given equation.

First, we add

`-7x`
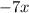
to both sides to obtain,


`- 7x + 7 x+ 3y = m - 7x`

This simplifies to,


`3y = m - 7x`

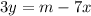
We divide both sides by 3 to get,


`y = (m - 7x)/(3)`

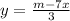
QUESTION 2

The given equation is,


`4(r + 3) = t`

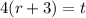
We want to make

`r`
the subject.

We first of all divide both sides by 4 to get,


`(4(r + 3))/(4) = (t)/(4)`

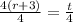
We now cancel out the common factor on the left hand side to get,


`r + 3 = (t)/(4)`

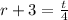
Let us add -3 to both sides of the equation to obtain,


`r + 3 + - 3 = (t)/(4) + - 3`


`r = (t)/(4) - 3`


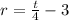
QUESTION 3

The given equation is


`2x + b = w`

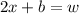
We want to solve for x, so we subtract b from both sides to obtain,


`2x + b - b = w - b`

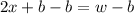
This simplifies to,


`2x = w - b`

We divide both sides by 2 to obtain,


`(2x)/(2) = (w - b)/(2)`

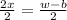
We cancel out common factors to get,


`x = (w - b)/(2)`

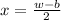
QUESTION 4

The given equation is


`x(1 + y) = 2`

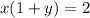
We want to solve for x, so we divide both sides by


`(1 + y)`
to obtain,


`(x(1 + y))/(1 + y) = (2)/(1 + y)`

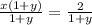
We cancel out the common factors to obtain,


`x = (2)/(1 + y)`