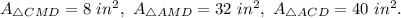If BM : MD = 1 : 4, then
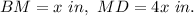 Triangles AMD and CMB are similar, then
Triangles AMD and CMB are similar, then
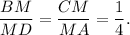
Let
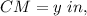 then
then
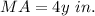
Given
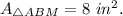 Note that
Note that
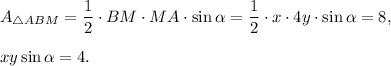
1. Consider triangle CMD. The area of this triangle is
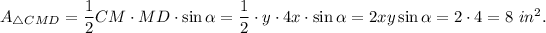
2. Consider triangle AMD. The area of this triangle is
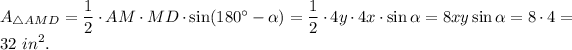
3. Consider triangle ACD. The area of this triangle is
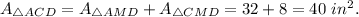
Answer: