ANSWER
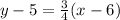 ,Yes
,Yes
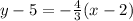 ,NO
,NO
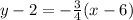 ,NO
,NO
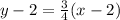 ,Yes
,Yes
Step-by-step explanation
The line passes through these two points,
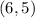 and
and
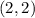 .
.
We can use these two points to determine the slope of the line.
The formula for finding the slope of a line when at least two points are known is
 .
.
We can choose
 and
and
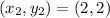 or
or
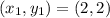 and
and
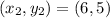 .
.
We shall get the same result.
 .
.
We now determine the equation of the line using the poit-slope formula,
 .
.
When we choose
 , then we will obtain,
, then we will obtain,
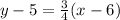 as the point-slope form.
as the point-slope form.
When we choose
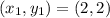 , then we will obtain,
, then we will obtain,
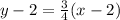 as the point-slope form.
as the point-slope form.