Question

The Moon (7.35 x 10^22 kg) is 3.85 x 10^8 m from the Earth and orbits around it in a circle. a) If the period of the Moon is 27.3 days, how fast is it moving in m/s? b) Find the centripetal force that the Earth exerts on the Moon. c) Identify the type of force that is the centripetal force.

Answer 1

a) Speed of the Moon: 1025 m/s

The speed of the moon is equal to the ratio between the circumference of its orbit and the orbital period:

`v=(2 \pi r)/(T)`

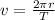
where

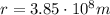`r=3.85\cdot 10^8 m` is the radius of the orbit of the Moon

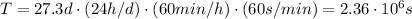`T=27.3 d \cdot (24 h/d) \cdot (60 min/h) \cdot (60 s/min)=2.36\cdot 10^6 s` is the orbital period

Substituting into the formula, we find

`v=(2 \pi (3.85\cdot 10^8 m))/(2.36\cdot 10^6 s))=1025 m/s`

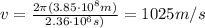
b) Centripetal force:
`2.0 \cdot 10^(20) N`

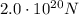
The centripetal force acting on the Moon is given by:

`F=m(v^2)/(r)`

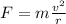
where

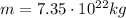`m=7.35 \cdot 10^(22)kg` is the mass of the Moon

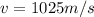`v=1025 m/s` is its orbital speed

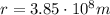`r=3.85\cdot 10^8 m` is the radius of the orbit

Substituting into the formula, we find

`F=(7.35 \cdot 10^(22) kg) ((1025 m/s)^2)/(3.85\cdot 10^8 m)=2.0 \cdot 10^(20) N`

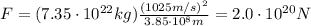
c) Gravitational force

The only relevant force that acts on the Moon, and that keeps the Moon in circular motion around the Earth, is the gravitational force exerted by the Earth on the Moon. In fact, this force "pulls" the Moon towards the Earth, so towards the centre of the orbit of the Moon, therefore it acts as source of centripetal force for the Moon.