Question

what is the slope intercept form of the linear equation with a graph that passes through (-4,7) and (6,-8)

Answer 1

Step-by-step explanation:

Slope-intercept form: →
`y=mx+b`

m: represents the slope and is constant.

b: represents the y-intercept.

The y-intercept is the point on a graph at which the graph crosses the y-axis.

You had to used rise/run.

`(rise)/(run)`

`m=(rise)/(run)`

`Slope=(y^2-y^1)/(x^2-x^1)`

`rise=y^2-y^1`

`run=x^2-x^1`

`(x^1,y^1)=(-4,6)`

`(x^2,y^2)=(7,-8)`

`rise=y^2-y^1=-8-7=-15`

`run=x^2-x^1=6--4=10`

`-15/10`

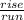
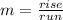
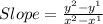
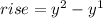
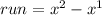
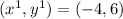
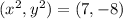
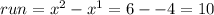
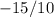
But the slope is -15.

But the y-intercept is 10.

Hope this helps!

Answer 2

The slope-intercept form:

`y=mx+b`

m - slope

`m=(y_2-y_1)/(x_2-x_1)`

b - y-intercept.

We have the points (-4, 7) and (6, -8). Substitute:

`m=(-8-7)/(6-(-4))=(-15)/(10)=-(3)/(2)`

Then, we have

`y=-(3)/(2)x+b`

Put the coordinates of the point (-4, 7) to the equation of line:

`7=-(3)/(2)(-4)+b\\\\7=3(2)+b\\\\7=6+b\quuad\text{subtract 6 from both sides}\\\\1=b`

Answer:

`y=-(3)/(2)x+1`