the lines are perpendicular
to determine which case is true we require the slope m of the lines
Parallel lines have equal slopes
Perpendicular slopes are the negative inverse of each other
to calculate m use the gradient formula
m = ( y₂ - y₁ ) / ( x₂ - x₁ )
with (x₁, y₁ ) = B(1, - 4 ) and (x₂, y₂ ) = T(5, 12 )
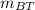 =
=
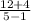 =
=
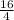 = 4
= 4
repeat with
(x₁, y₁ ) = M(-8, 3 ) and (x₂, y₂ ) = V(-4, 2 )
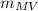 =
=
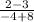 = -
= -

4 and -
 are negative inverses, hence
are negative inverses, hence
BT and MV are perpendicular to each other