Question

which expressions are equivalent to the first one? I don't understand how to determine that so please explain. Thanks!​

Answer 1

9514 1404 393

Answer:

(a) -(x+7)/y

(b) (x+7)/-y

Explanation:

There are several ways you can show expressions are equivalent. Perhaps the easiest and best is to put them in the same form. For an expression such as this, I prefer the form of answer (a), where the minus sign is factored out and the numerator and denominator have positive coefficients.

The given expression with -1 factored out is ...

`(-x-7)/(y)=(1(x+7))/(y)=\boxed{-(x+7)/(y)} \quad\text{matches A}`

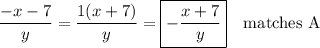
Likewise, the expression of (b) with the minus sign factored out is ...

`(x+7)/(-y)=\boxed{-(x+7)/(y)}`

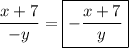
On the other hand, simplifying expression (c) gives something different.

`(-x-7)/(-y)=(-(x+7))/(-(y))=(x+7)/(y) \qquad\text{opposite the given expression}`

__

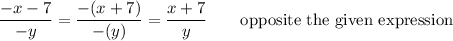
Another way you can write the expression is term-by-term with the terms in alpha-numeric sequence (so they're more easily compared).

Given: (-x-7)/y = (-x/y) +(-7/y)

(a) -(x+7)/y = (-x/y) +(-7/y)

(b) (x+7)/(-y) = (-x/y) +(-7/y)

(c) (-x-7)/(-y) = (x/y) +(7/y) . . . . not the same.

__

Of course, you need to know the use of the distributive property and the rules of signs.

a(b+c) = ab +ac

-a/b = a/(-b) = -(a/b)

-a/(-b) = a/b

__

Summary: The given expression matches (a) and (b).

_____

Additional comments

Sometimes, when I'm really stuck trying to see if two expressions are equal, I subtract one from the other. If the difference is zero, then I know they are the same. Looking at (b), we could compute ...

`\left((-x-7)/(y)\right)-\left((x+7)/(-y)\right)=(-y(-x-7)-y(x+7))/(-y^2)\\\\=(xy+7y-xy-7y)/(-y^2)=(0)/(-y^2)=0`

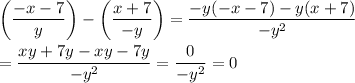
Yet another way to check is to substitute numbers for the variables. It is a good idea to use (at least) one more set of numbers than there are variables, just to make sure you didn't accidentally find a solution where the expressions happen to be equal. We can use (x, y) = (1, 2), (2, 3), and (3, 5) for example.

The given expression evaluates to (-1-7)/2 = -4, (-2-7)/3 = -3, and (-3-7)/5 = -2.

(a) evaluates to -(1+7)/2 = -4, -(2+7)/3 = -3, -(3+7)/5 = -2, same as given

(b) evaluates to (1+7)/-2 = -4, (2+7)/-3 = -3, (3+7)/-5 = -2, same as given

(c) evaluates to (-1-7)/-2 = 4, different from given