Question

PLZ HELP

what is the equation of a line, in point-slope form, that passes through (5,-3) and has a slope of 2/3

A.
y + 5 = 2/3 (x - 3)

B.
y - 3 = 2/3 (x + 5)

C.
y - 5 = 2/3 (x + 3)

D.
y + 3 = 2/3 (x - 5)

Answer 1

D. is the correct answer.

Slope intercept form:
`y=mx+b`

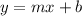
m: represents the slope and is constant.

b: represents the y-intercept.

Given the following equation, locate the slope and y-intercept of the line.

For example:
`y=-(1)/(2)x-8`

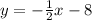
The slope: m=
`-(1)/(2)`

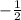
The y-intercept: b=
`-8`

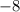
Point slope form: →
`slope=(y^2-y^1)/(x^2-x^1)`

`m=(y^2-y^1)/(x^2-x^1)`

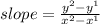
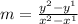
Used: rise/run

`m=(rise)/(run)`

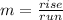
Given:

`(y^1)=m(x^1)`

`y-3=(2)/(3)(x-5)`

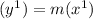
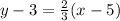
Then you add by the variable on y-3.

`\boxed{y+3=2/3(x-5)}`

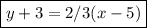
Hope this helps!

Thanks!

Have a great day!

Answer 2

point slope form

y-y1 = m(x-x1)

y--3 = 2/3(x-5)

y+3=2/3(x-5)

Choice D