Answer:
Given the equation:
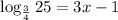
Solve for x;
Use logarithmic rules:
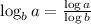
Then;
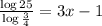
Using values of:
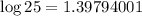
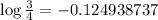
Substitute these values we have;
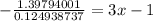
Simplify:
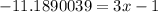
Add 1 to both sides we get;
-10.1890039 = 3x
Divide both sides by 3 we get;
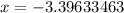
Therefore, the approximate value of x in the equation
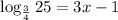 is -3.396
is -3.396