Question

Suppose that g (x) varies inversely with x and g (x)=0.2 when x = 0.1.

What is g (x) when x = 1.6?

0.0125
0.032
0.02
0.06

Answer 1

A. 0.0125

Explanation:

0.2*0.1= 0.02

.02/1.6 = 0.0125

Took the test and got it correct

Answer 2

Answer : 0.0125

Suppose that g (x) varies inversely with x and g (x)=0.2 when x = 0.1.

If x varies inversely with y then y=k/x

Where k is constant of proportionality

g (x) varies inversely with x , so
`g(x) = (k)/(x)`

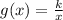
g (x)=0.2 when x = 0.1

Plug in the values and solve for k

`g(x) = (k)/(x)`

`0.2 = (k)/(0.1)`

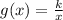
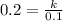
Multiply 0.1 on both sides

0.02 = k

so
`g(x) = (0.02)/(x)`

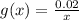
Now we need to find g(x) when x= 1.6

Plug in 1.6 for x and find out g(x) in the above equation

`g(x) = (0.02)/(1.6)`

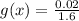
g(x)= 0.0125