Answer:
Given: Diameter of cone = 38 feet and height of cone = 14 feet.
Volume of cone V with radius r is one-third the area of the base B times the height h.
i,e
 =
=
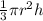 ......[1]
......[1]
,where B =

First find the radius(r);
Using Diameter(D) = 2r
38 =2r
Divide both side by 2 we get;
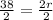
Simplify:
19 = r
or r =19 feet
Now, substitute the value of r = 19 feet and h = 14 feet in [1] [ Use value of
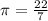 ]
]
then, we have:
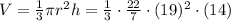
or
V =
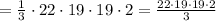
or
V =
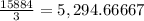 ≈ 5,294.67 cubic feet.
≈ 5,294.67 cubic feet.
therefore, the volume of pile is; ≈ 5,294.67 cubic feet.