Question

Jesse places a mirror on the ground 25 ft from the base of a light pole. He walks backward until he can see the top of the light pole in the middle of the mirror. At that point, Jesse’s eyes are 6 ft above the ground and he is 5.5 ft from the mirror. Draw a sketch of this situation and use similar triangles to find the height of the light pole. Round to the nearest tenth. PLEASE HELP

Answer 1

Suppose light pole is at PQ.

Jesse is at RS.

Mirror is at M.

In the diagram; PQ = h, QM = 25 feet, RS = 6 feet, SM = 5.5 feet.

We know angle of incidence = angle of reflection, so ∠i = ∠r.

It means ∠x = ∠a

and 90-x = 90-a ⇒ ∠y = ∠b

∠Q = ∠S = 90°

It means triangle ΔPQM is similar to triangle ΔRSM.

So, Ratio of corresponding sides would be proportional.

`(PQ)/(QM) =(RS)/(SM) \\(h)/(25) =(6)/(5.5) \\Using \;Cross \;Multiplication\\5.5*h = 25*6\\5.5h = 150\\Dividing \;both \;sides \;by \;5.5\\(5.5h)/(5.5) =(150)/(5.5) \\h = (1500)/(55) \\h = (300)/(11) =27.27272727 \approx 27.3 \;feet`

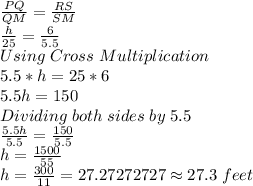
Hence, the height of the light pole is 27.3 feet.