Answer:
The correct option is C.
Explanation:
The function has axis of symmetry at
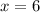 , it represents that the parabola is along the x-axis and the standard form of parabola is
, it represents that the parabola is along the x-axis and the standard form of parabola is
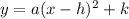
Where, a is scale factor and (h,k) is vertex.
The maximum or minimum value of a quadratic function is the vertex of parabola. So, vertex of parabola is (6,4).
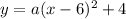
The y-intercept of the function is (0,-32)
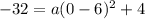
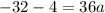
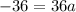

Therefore required equation of parabola is
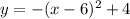

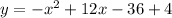
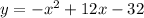
Therefore option C is correct.