Question

Write the equation of a line perpendicular to 2y+x=4 and passes through the point (2,1) ​

Answer 1

`-2x+y=-3`

Explanation:

Recall perpendicular lines have negative-reciprocal slopes. Since the equation
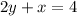`2y+x=4` has a slope of
`-(1)/(2)` (
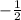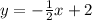`y=-(1)/(2)x+2`), any line perpendicular to it will have a slope of
`-(1)/(-(1)/(2))=2`.

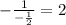Therefore, we have the line:

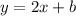`y=2x+b` where
`b` is the y-intercept.

We can plug in the point it passes through to find the final equation:

`1=2(2)+b,\\b=1-4,\\b=-3`.

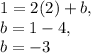Therefore, the equation of the line perpendicular to
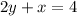`2y+x=4` that passes through the point
`(2, 1)` is:

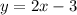`y=2x-3` (slope-intercept form)

However, since the initial line given is in standard form, re-write this equation to standard form:

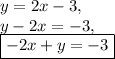`y=2x-3,\\y-2x=-3,\\\fbox{$-2x+y=-3$}`.

Answer 2

Por favor, dame una captura de pantalla de la pregunta No entiendo esto gracias