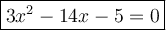Question

Write a quadratic equation given the roots -1/3 and 5, show your work

Answer 1

`\boxed{(x - a)(x - b) = 0}`

The equation above is the intercept form. Both a-term and b-term are the roots of equation.

`x = - (1)/(3) \\ x = 5`

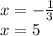
These are the roots of equation. Therefore we substitute a = - 1/3 and b = 5 in the equation.

`(x + (1)/(3) )(x - 5) = 0`

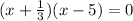
Here we can convert the expression x+1/3 to this.

`x + (1)/(3) = 0 \\ 3x + 1 = 0`

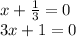
Rewrite the equation.

`(3x + 1)(x - 5) = 0`

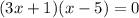
Simplify by multiplying both expressions.

`3 {x}^(2) - 15x + x - 5 = 0 \\ 3 {x}^(2) - 14x - 5 = 0`

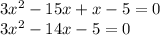
Answer Check

Substitute the given roots in the equation.

`3 {(5)}^(2) - 14(5) - 5 = 0 \\ 75 - 70 - 5 = 0 \\ 75 - 75 = 0 \\ 0 = 0`

`3( - (1)/(3) )^(2) - 14( - (1)/(3)) - 5 = 0 \\ 3( (1)/(9) ) + (14)/(3) - 5 = 0 \\ (1)/(3) + (14)/(3) - (15)/(3) = 0 \\ (15)/(3) - (15)/(3) = 0 \\ 0 = 0`

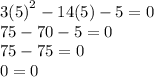
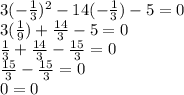
The equation is true for both roots.

Answer

`\large \boxed {3 {x}^(2) - 14x - 5 = 0}`