Question

School x and school y play each other in a competition. School X has 8 more points than school Y. School X has 3 times as many points as school y. How many points does each school have?

Answer 1

Answer: X = 12 points and Y = 4 points.

Explanation:

Answer 2

Let the points for School X be a

and for the School Y be b.

From the given condition : School X has 8 more points than school Y.

we have;

a = b+8 ......[1]

Also, School X has 3 times as many points as school Y, which implies

a = 3b ......[2]

Substitute the value a of [2] in [1]; to solve for b;

we have;

3b=b+8

Subtract b from both sides of an equation we get;

3b-b=b+8-b

Simplify:

2b=8

Divide by 2 from both sides of an equation we get;

`(2b)/(2)= (8)/(2)`

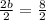
Simplify:

b=4

Substitute the value of b in equation [2];

`a=3 \cdot 4 = 12`

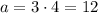
Therefore, School X has 12 points and School Y has 4 points.