Answer: At 24 February, 2014 the population gets twice of its initial population.
Step-by-step explanation:
Since we have given that
The population for Alpha City, t years after January 1, 2004 is given as
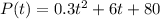
First we find out the initial population, i.e. t=0,
So, our quadratic equation becomes,
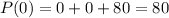
According to question, we have said that if the population has twice its initial population, then it becomes
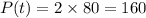
So, time taken to reach this above mentioned population is given by

Now, we know that time can't be negative so, we take t=9.149 years.
Hence, At 24 February, 2014 the population gets twice of its initial population.