csc θ = 13/5
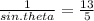
When you flip both sides:
sin θ = 5/13
If you know the Pythagorean triples, it will be 5, 12, and 13. Otherwise you could do a² + b² = c²
You can use:
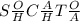
which is
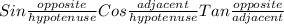
Or you could draw a triangle, either way works.
To find tangent, you know 13 is the hypotenuse because it is the longest side, and 5 is "opposite" so 12 is "adjacent. So:
tan theta = 5/12
And cosine is adjacent/ hypotenuse, so it is:
cos theta = 12/13
sec theta is the opposite of cos theta, so it is:
sec theta = 13/12
B and C are correct