Question

The function f(x) = 4(4)x represents the growth of a fly population every year in a remote swamp. Jackie wants to manipulate the formula to an equivalent form that calculates three times a year, not just once a year. Which function is correct for Jackie's purpose, and what is the new growth rate?

Answer Options:

f(x) = 4(4)^x; growth rate 400%

f(x) = 4(4)^3x; growth rate 4%

f(x) = 4(1.59)^3x; growth rate 59%

f(x) = 4(1.59)^x; growth rate 4%

Answer 1

59%

Explanation:

^^

Answer 2

The function f(x) = 4(4)x represents the growth of a fly population every year in a remote swamp.

calculates three times a year, not just once a year.

`f(x)= 4(4)^x`

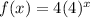
3 times a year

so x becomes 3x

`f(x)= 4(1+r)^(3x)`

`4(4)^x=4(1+r)^(3x)`

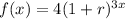
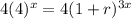
Take log on both sides

`log(4)^x=log(1+r)^(3x)`

`log(4)^x=log(1+r)^(3x)`

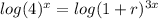
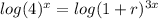
Use log property and move exponent before log

`xlog(4)=3xlog(1+r)}`

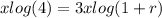
Divide both sides by x

log 4 = 3 log(1+r)

Solve for '1+r'

log 4 = log(1+r)^3

Remove log from both sides

4 = (1+r)^3

take cube root on both sides

1.584740= 1+r

1+r = 1.59

`f(x)= 4(1+r)^(3x)`

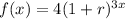
so equation becomes

`f(x)= 4(1.59)^(3x)`

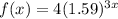
1+r = 1.59

subtract 1 from both sides

So r= 59 = 59%

So growth factor is 59%

Answer is option C