Question

Okay so i dont have the best grade in math grade in math so help?

what is the slope? shown work do need to be shown

Answer 1

You use the slope formula:

`m = (y_(2)-y_(1))/(x_(2)-x_(1))`

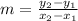
And you plug in the points. The first point is (-4,4), and the second point is (0,-1)

y₂ is the second y value/coordinate (which is -1)

y₁ is the first y value/coordinate (which is 4)

x₂ is the second x value/coordinate (which is 0)

x₁ is the first x value/coordinate (which is -4)

`m = (y_(2)-y_(1))/(x_(2)-x_(1))`

`m = (-1 - 4)/(0 - (-4))`

`m = (-1 - 4)/(0 + 4)`

`m = (-5)/(4)`

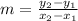
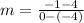
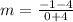
That is your slope