Answer:
4,410
Explanation:
So we can use the compound interest formula:
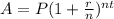 where P = initial investment, r = interest rate (in decimal form), n = number of compounds in the time unit, t = time unit
where P = initial investment, r = interest rate (in decimal form), n = number of compounds in the time unit, t = time unit
But we don't really need to use this formula since it might just be a bit easier to understand what this compound interest means, it's also a bit easier since it's only annually.
So at a 5% compound annual interest compounded annually, this means that after every year the total amount has 5% added to it, or in other words the new amount is 105%
So after one year it's:
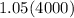 , the next year the new amount is 105% of the previous year, or 5 percent more. So it's essentially:
, the next year the new amount is 105% of the previous year, or 5 percent more. So it's essentially:
 which just simplifies to:
which just simplifies to:

We could've also used the formula where:
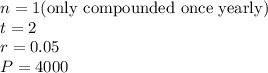
To get the formula:
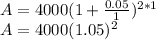
which is essentially the same thing and would've resulted in the same answer.