Question

If $4,000 is invested at 5% interest compound annually, how much will the investment be worth after 2 years

Answer 1

4,410

Explanation:

So we can use the compound interest formula:
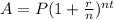`A=P(1+(r)/(n))^(nt)` where P = initial investment, r = interest rate (in decimal form), n = number of compounds in the time unit, t = time unit

But we don't really need to use this formula since it might just be a bit easier to understand what this compound interest means, it's also a bit easier since it's only annually.

So at a 5% compound annual interest compounded annually, this means that after every year the total amount has 5% added to it, or in other words the new amount is 105%

So after one year it's:
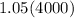`1.05(4000)`, the next year the new amount is 105% of the previous year, or 5 percent more. So it's essentially:
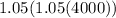`1.05(1.05(4000))` which just simplifies to:
`4,410`

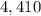
We could've also used the formula where:
`n=1 \text{(only compounded once yearly)}\\t=2\\r=0.05\\P=4000`

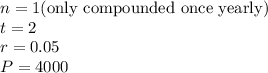
To get the formula:
`A=4000(1+(0.05)/(1))^(2*1)\\A=4000(1.05)^2`

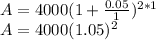
which is essentially the same thing and would've resulted in the same answer.