Given function is
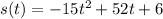
where t is the time in seconds and s(t) is the height of the firework in t seconds.
Given that height of the firework is 45 feet. Now we have to find when it happens that is find value of t when s(t)=45
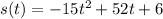
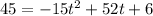

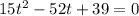
Apply quadratic formula
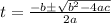
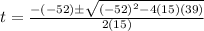
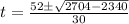
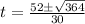
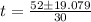
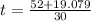 or
or
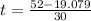
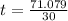 or
or
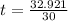
 or
or
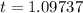
Hence final answer is 2.3693 seconds and 1.09737 seconds.
Two answers means height of 45 feet will be attained two times.