Question

Suppose that you lowered the temperature of a gas from 100˚C to 50 ˚C. By what factor do you change the volume of the gas?

Answer 1

Lowering the temperature of a gas from 100°C to 50°C, while keeping pressure constant, will cause the gas volume to decrease to approximately 86.6% of its original value, in accordance with Charles's Law.

Step-by-step explanation:

When you lower the temperature of a gas from 100°C to 50°C, the volume of the gas will decrease as well, given that the pressure remains constant. This is an application of Charles's Law, which states that the volume of a gas is directly proportional to its temperature (in Kelvin). To find the factor by which the volume changes, one must convert the temperatures to Kelvin and then divide the final temperature by the initial temperature.

Converting 100°C to Kelvin: 100 + 273.15 = 373.15 K

Converting 50°C to Kelvin: 50 + 273.15 = 323.15 K

The factor by which the volume changes is 323.15 K / 373.15 K, which simplifies to approximately 0.866. Hence, the volume of the gas decreases to about 86.6% of its original value.

Answer 2

Answer:- Volume decreases by a factor of 1.15.

Solution:- At constant pressure, volume of the gas is directly proportional to the the kelvin temperature.

The equation is written as:

`(V_1)/(T_1)=(V_2)/(T_2)`

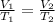
where,
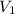`V_1` is the volume at initial temperature
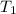`T_1` and
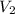`V_2` is the volume at final temperature
`T_2` .

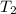Temperature must be in kelvins. So, let's convert both the temperatures to kelvin.

To convert degree C to kelvin we add 273.

So,
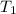`T_1` = 100 + 273 = 373 K

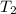`T_2` = 50 + 273 = 323 K

The equation could also be written as:-

`(V_1)/(V_2)=(T_1)/(T_2)`

`(V_1)/(V_2)=(373)/(323)`

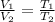
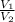`(V_1)/(V_2)` = 1.15

From here we could say that the volume decreases by a factor of 1.15.

For example if the initial volume
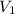`V_1` is 1 L then final volume
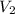`V_2` will be
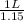`(1L)/(1.15)` that is 0.87 L.