Question

The mean price for a home in a Florida county is $125,000. The standard deviation for the same sample is $23,000. What percentage of homes in the county are valued over $100,000? Use the Standard Normal Probabilities table to find your answer. Enter your answer with two places.

I keep getting 86.15%
The answer is supposed to be 86.21%

I am not sure what I did wrong so please explain what you did.

Answer 1

Solution: There is nothing wrong with your calculation's. But the question wants to round the z score to two decimal places.

Let me show you how to get 86.21%.

We are given:

`\mu=125,000`

`\sigma=23,000`

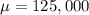
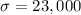
We have to find
`P(x>100,000)`

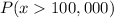
Using the z-score formula, we have:

`z=(x-\mu)/(\sigma)`

`=(100,000-125,000)/(23,000)`

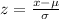
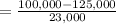
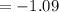`=-1.09` rounded to two decimal places

Now we have to find
`P(z>-1.09)`

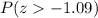
Using the standard normal table, we have:

`P(x>100,000)=P(z>-1.09) = 0.8621` rounded to 4 decimal places

`=86.21\%`

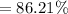
Therefore, the percentage of homes in the county that are valued over $100,000 is 86.21%