I'm assuming you're asked to find the equations for lines that fit the given descriptions.
In the first case, having no x-intercept means that the line must be horizontal and not
 , so it will be entirely determined by the y-intercept, which is -5. So the line has equation
, so it will be entirely determined by the y-intercept, which is -5. So the line has equation
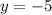 .
.
In the second case, the line is parallel to
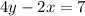 , or equivalently
, or equivalently
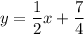 , which has slope
, which has slope
 . Parallel lines have the same slope. With the point-slope formula, you can find its equation:
. Parallel lines have the same slope. With the point-slope formula, you can find its equation:
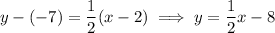
In the third case, the line is perpendicular to
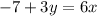 , or
, or
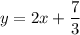 . Perpendicular lines have slopes that are negative reciprocals of one another. Here, the given line has slope 2, which means the slope of its perpendicular counterpart is
. Perpendicular lines have slopes that are negative reciprocals of one another. Here, the given line has slope 2, which means the slope of its perpendicular counterpart is
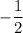 . Point-slope formula again:
. Point-slope formula again:
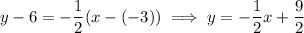
In the fourth case, you first need to find the slope of such a line. Note that the x-coordinates are the same, which means the line will be vertical and the equation is determined entirely by the x-intercept. So the equation is
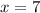 .
.