Answer:
1. The equation of parabola is
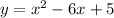 .
.
2. The equation of parabola is
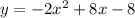 .
.
Explanation:
1.
Let the equation of parabola be
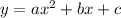
It is given that the parabola passing through points (0,5), (2,-3) and (-1,12).
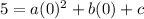
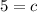
The value of c is 5.

The equation must be satisfied by the points (2,-3) and (-1,12).
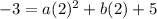

Divide both sides by 2.
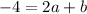 .... (1)
.... (1)
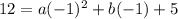
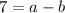 .... (2)
.... (2)
From (1) and (2), we get

Therefore equation of parabola is
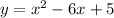 .
.
2.
Let the equation of parabola be
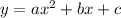
It is given that the parabola passing through points (2,0), (3,-2) and (1,-2).
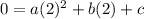
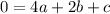 .... (3)
.... (3)
The equation must be satisfied by the points (3,-2) and (1,-2).

 .... (4)
.... (4)

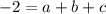 .... (5)
.... (5)
On solving (1), (2) and (3), we get
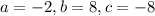
Therefore equation of parabola is
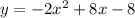 .
.