The function f(t) = 7 cos(pi over 4t) + 12 represents the tide in Light Sea. It has a maximum of 19 feet when time (t) is 0 and a minimum of 5 feet. The sea repeats this cycle every 8 hours
To find the height of the tide after 2 hours, we plug in 2 for t and find out f(2)
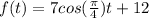
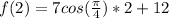
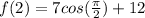
We know that cos (pi/2) is 0
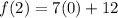
So f(2)= 12
After two hours, the height of the tide is 12 feet