Question

Which graph represents the piecewise-defined function?

y={−4/5x−3   if  x<0
{3x−10   if  x≥2

Answer 1

LAST GRAPH is right

Step-by-step explanation

Answer 2

Answer: The first option is correct.

Step-by-step explanation:

The given piecewise function is,

`y=\begin{cases}-(4)/(5)x-3 & \text{ if } x<0\\3x-10 & \text{ if } x\geq2 \end{cases}`

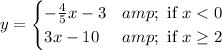
From the piecewise function we can say that if x<0, then

`f(x)=-(4)/(5)x-3`

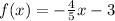
If
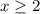`x\geq2`, then

`f(x)=3x-10`

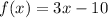
Since the f(x) is defined for x<0 and
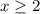`x\geq2`, therefore the function f(x) is not defined for
`0\leq x<2`.

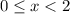In the graph 2, 3 and 4 for each value of x there exist a unique value of y, therefore the function is defined for all values of x, which is not true according to the given piecewise function.

Only in figure the value of y not exist when x lies between 0 to 2, including 0. It means the function is not defined for
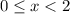`0\leq x<2`, hence the first option is correct.