Answer: The correct option is 1.
Step-by-step explanation:
The given piecewise function is,
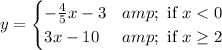
It means if x<0, then

If
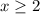 , then
, then
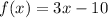
Since the f(x) is defined for x<0 and
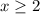 , therefore the function f(x) is not defined for
, therefore the function f(x) is not defined for
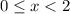 .
.
From the graph 2, 3 and 4 we can easily noticed that for each value of x there exist a unique value of y, therefore the function is defined for all values of x, which is not true according to the given piecewise function.
Only in figure the value of y not exist when x lies between 0 to 2, including 0. It means the function is not defined for
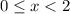 , hence the first option is correct.
, hence the first option is correct.