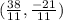Question

In the xy-coordinate plane, the coordinates of point of point S are (-2, -6), and the coordinates of point T are (18, 9). point Q lies on line segment ST so that the ratio of the distance from point S to point Q to the distance from point Q to point T is 3 to 5. What are the coordinates of Point Q? Do not round.

Q (, )

Work Shown or Explanation:

Answer 1

find the distance between S and T

`d=√((-2-18)^2+(-6-9)^2)`

`d=25`

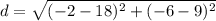
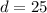
so i distance is ratio o 3:8

3+8=11

25/11=25/11

3*25/11=75/11

8*25/11=200/11

the distance from S to Q is 75/11 and distance rom Q to T is 200/11

if (x,y) is point Q

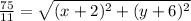`(75)/(11)=√((x+2)^2+(y+6)^2)` is a circle made up of points where Q is 75/11 units away from S

if we find the equation of the line ST and find the intersection of the line and this circle, we can ind the point Q

or (-2,-6) and (18,9), slope is (-6-9)/(-2-18)=-15/-20=3/4

y=3/4x+b, if we put (-2,-6) in we get that b=-9/2

y=3/4x-9/2

if we subsitute for y we get

`(75)/(11)=\sqrt{(x+2)^2+((3)/(4)x-(9)/(2)+6)^2}`

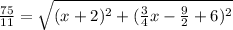
if we solve this by squareing both sides and doing some algebraeic stuff we get 2 points (because the line crosses the circle at 2 points):

(-82/11,-111/11) and (38/11,-21/11)

we have to pick the one between S and T, check the y value

the irst point has a y value of -10.0909 which is below S, so this isn't the point

the 2n point has a vaue of -1.90909 and this is between -6 and 9 so this is the point

Q is
`((38)/(11),(-21)/(11))`